Sin inmutarse después de tres décadas de búsqueda, y con la ayuda de una supercomputadora, los matemáticos finalmente descubrieron un nuevo ejemplo de un número entero especial llamado número de Dedekind. Solo el noveno de su tipo, o D(9), se calcula que es igual a 286 386 577 668 298 411 128 469 151 667 598 498 812 366, si estás actualizando tus propios registros. Este monstruo de 42 dígitos sigue al D(8) de 23 dígitos descubierto en 1991.
Comprender el concepto de un número de Dedekind es difícil para los no matemáticos, y mucho menos resolverlo. De hecho, los cálculos involucrados son tan complejos e involucran números tan grandes que no era seguro que alguna vez se descubriera D(9).
“Durante 32 años, el cálculo de D(9) fue un desafío abierto, y era cuestionable si alguna vez sería posible calcular este número”, dice el científico informático Lennart Van Hirtum, de la Universidad de Paderborn en Alemania.
En el centro de un número de Dedekind están las funciones booleanas, o un tipo de lógica que selecciona una salida de las entradas compuestas de solo dos estados, como un verdadero y un falso, o un 0 y un 1. Las funciones booleanas monótonas son aquellas que restringen la lógica de tal manera que cambiar un 0 por un 1 en una entrada solo hace que la salida cambie de 0 a 1, y no de 1 a 0. Los investigadores lo describen usando colores rojo y blanco en lugar de 1s y 0s, pero la idea es la misma.
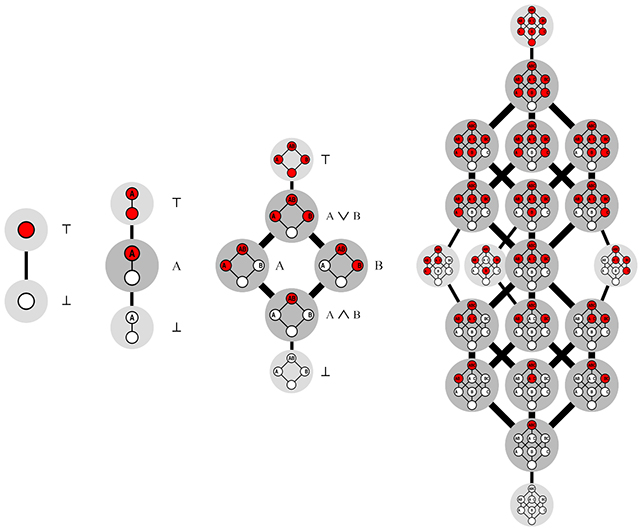
“Básicamente, puedes pensar en una función booleana monótona en dos, tres e infinitas dimensiones como un juego con un cubo de n dimensiones”, dice Van Hirtum.
“Equilibras el cubo en una esquina y luego coloreas cada una de las esquinas restantes de blanco o rojo”.
“Solo hay una regla: nunca debes colocar una esquina blanca sobre una roja. Esto crea una especie de intersección vertical roja-blanca. El objetivo del juego es contar cuántos cortes diferentes hay”.
Los primeros son bastante sencillos. Los matemáticos cuentan D(1) como 2, luego 3, 6, 20, 168…
En 1991, una supercomputadora Cray-2 (una de las supercomputadoras más poderosas de la época) y el matemático Doug Wiedemann necesitaron 200 horas para descifrar D(8). D(9) terminó siendo casi el doble de largo que D(8) y requirió un tipo especial de supercomputadora: una que usa unidades especializadas llamadas Field Programmable Gate Arrays (FPGA) que pueden realizar múltiples cálculos en paralelo. Eso llevó al equipo a la supercomputadora Noctua 2 en la Universidad de Paderborn.
“Resolver problemas combinatorios difíciles con FPGA es un campo de aplicación prometedor y Noctua 2 es una de las pocas supercomputadoras en todo el mundo con las que el experimento es factible”, dice el científico informático Christian Plessl, director del Paderborn Center for Parallel Computing (PC2) donde se guarda la Noctua 2.
Se requirieron más optimizaciones para darle a la Noctua 2 algo con lo que trabajar. Usando simetrías en la fórmula para hacer que el proceso sea más eficiente, los investigadores le dieron a la supercomputadora una gran suma para calcular, una suma que involucraba 5.510^18 términos (la cantidad de granos de arena en la Tierra se estima en 7.510^ 18, por comparar).
Después de cinco meses, Noctua 2 encontró una respuesta y ahora tenemos D(9). Los investigadores no han hecho ninguna referencia a D(10) por el momento, pero podemos imaginar que podría llevar otros 32 años encontrarlo. Hasta el momento no hay ningún documento que informe sobre la investigación, pero se presentará en septiembre en el Taller internacional sobre funciones booleanas y sus aplicaciones (BFA) que se llevará a cabo en Noruega.
Fuente: Science Alert.
